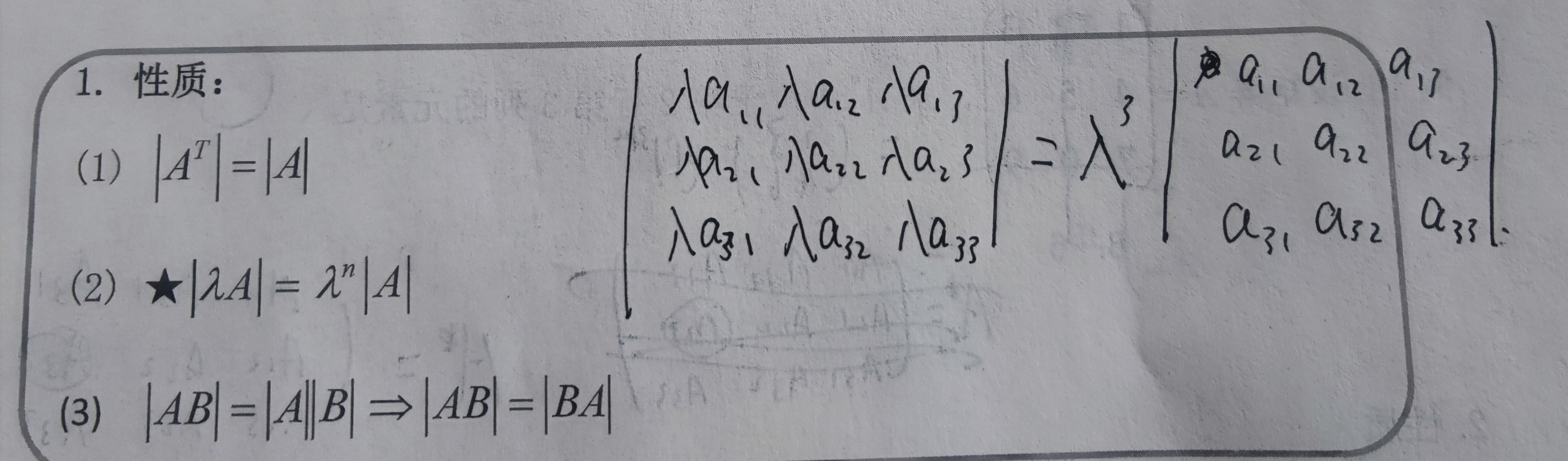

(若f(-x)=f(x)=>f(-x)-f(x)=0,则f(x)为偶函数, 若f(-x)=f(x)=>f(-x)+f(x)=0,则f(x)为奇函数)




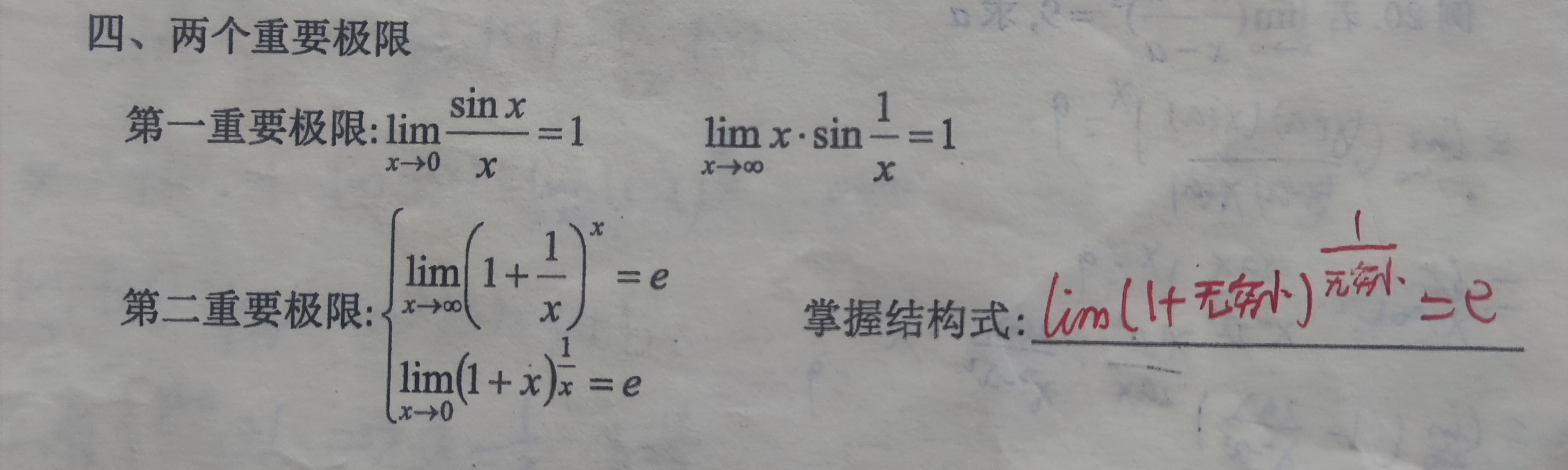
(f(x)在x0处有定义, x->x0时极限存在, 左极限=右极限)
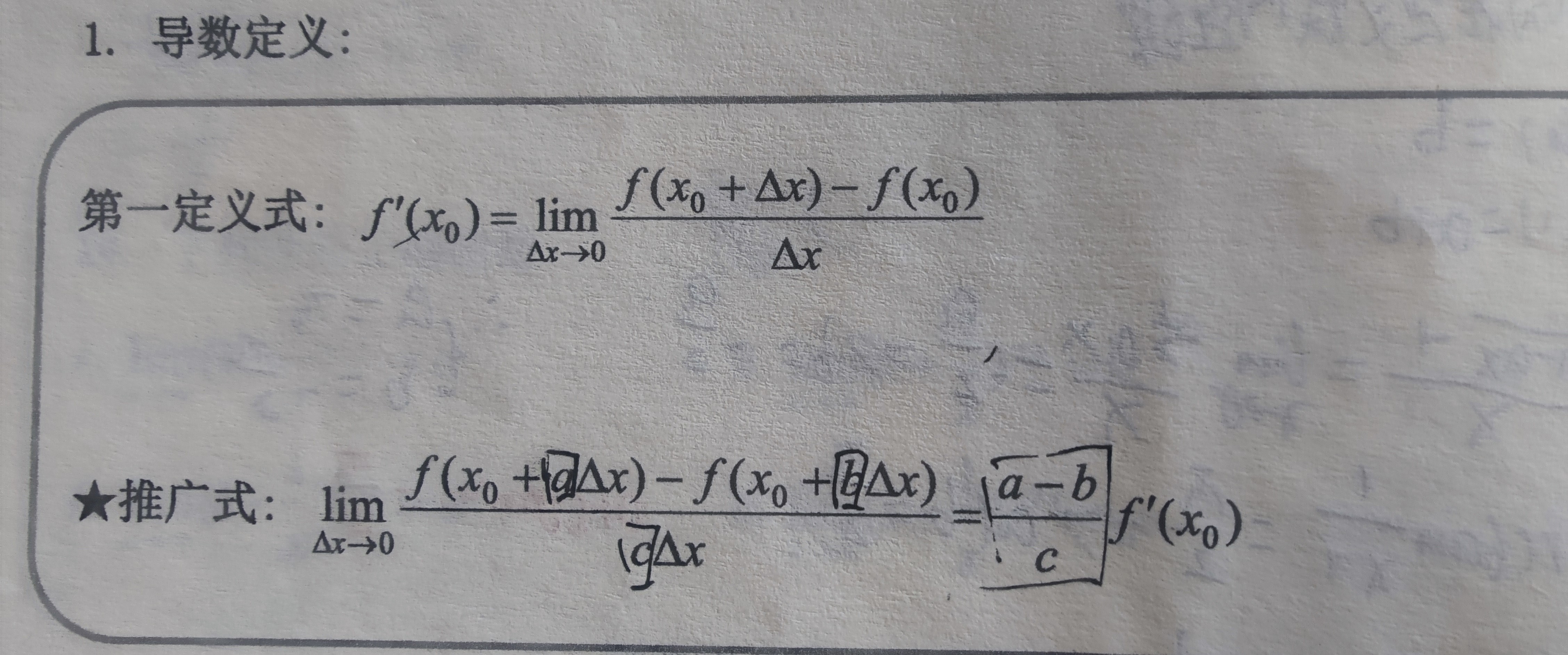
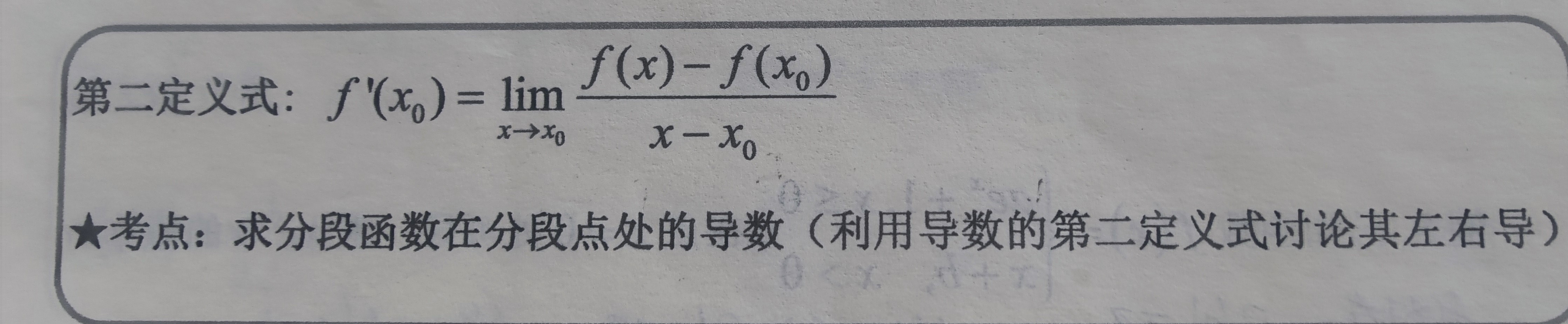
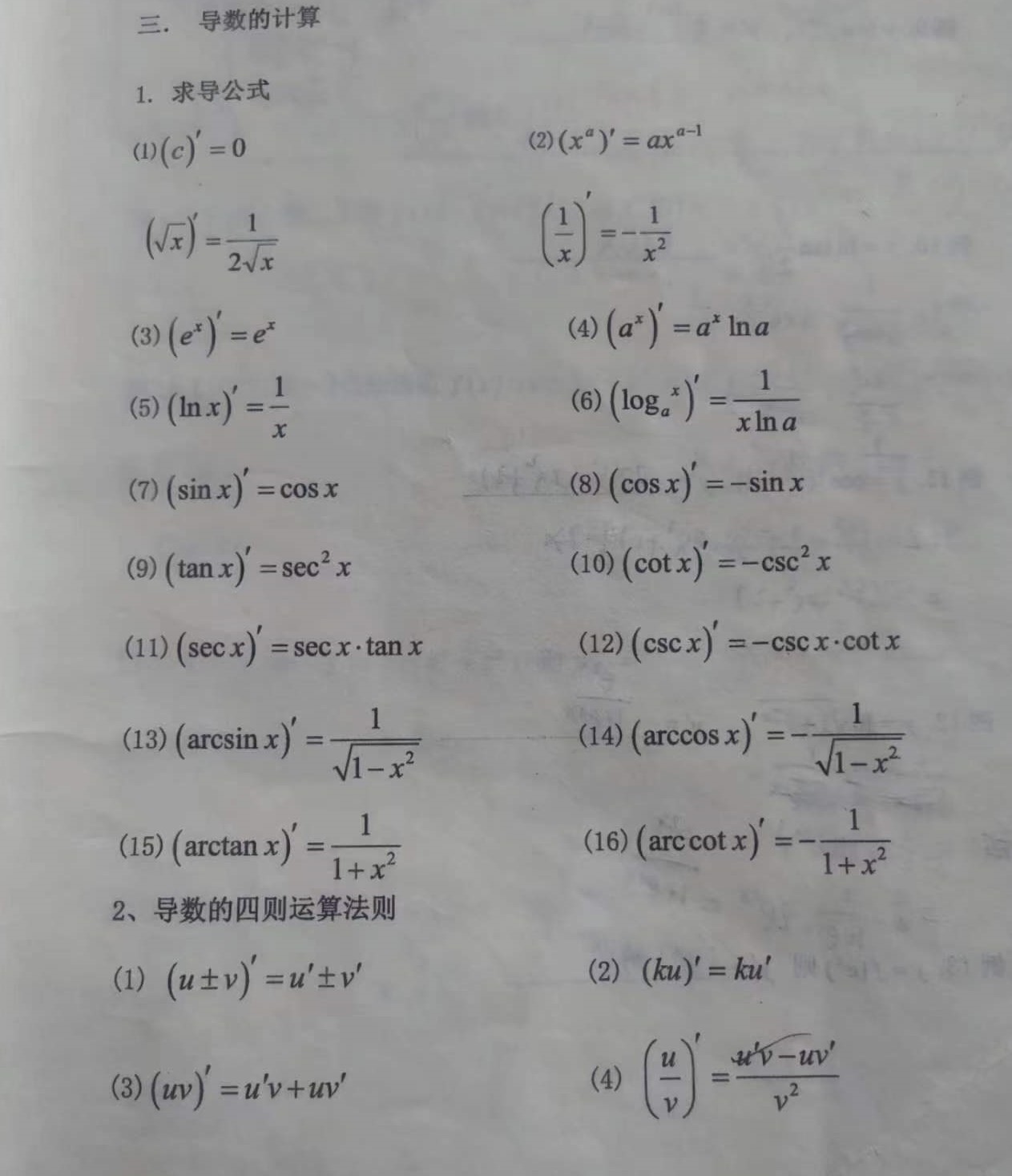

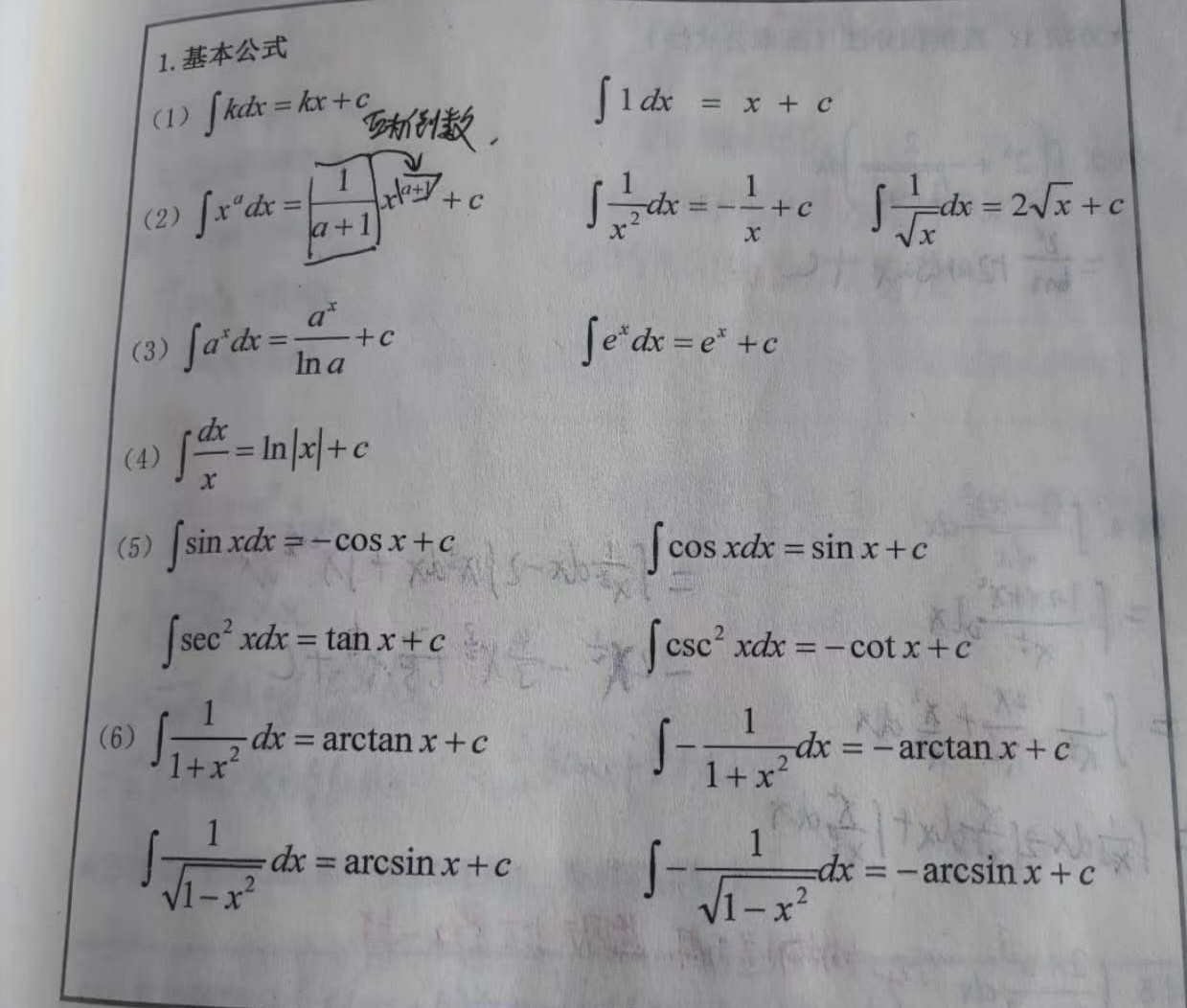
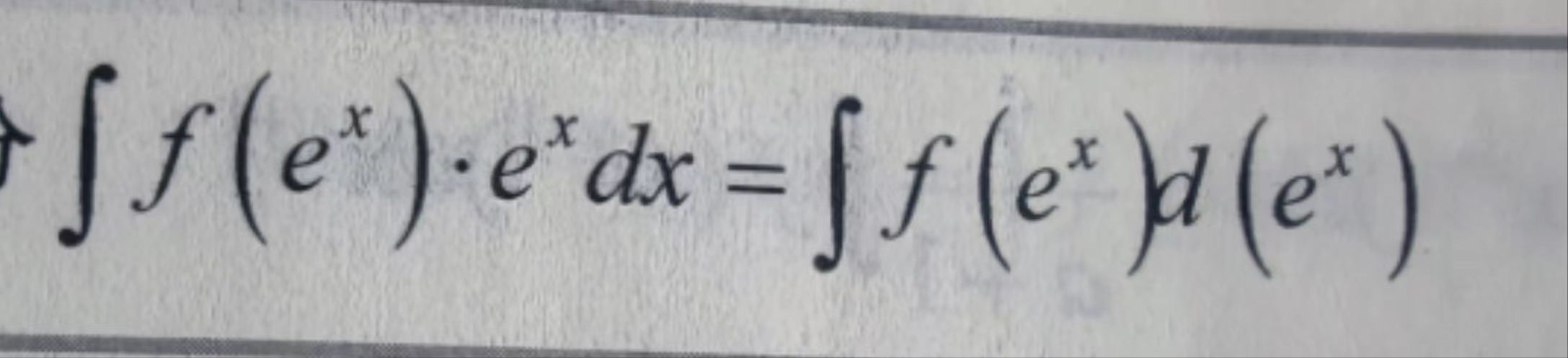
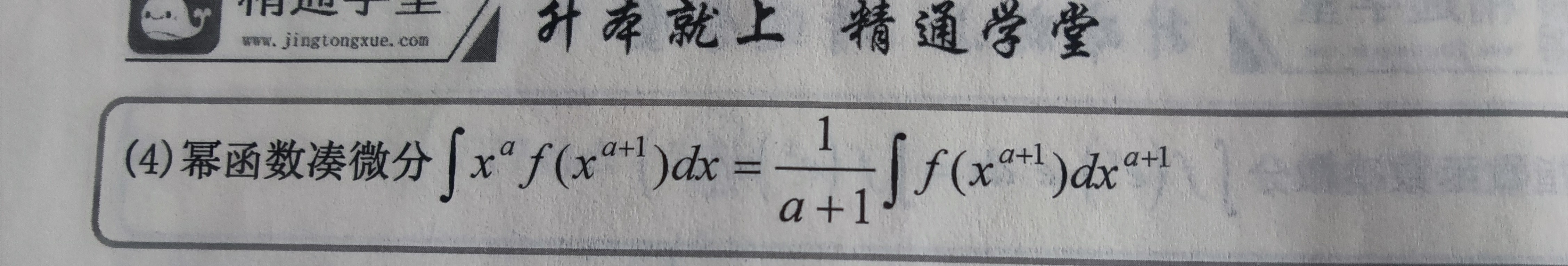
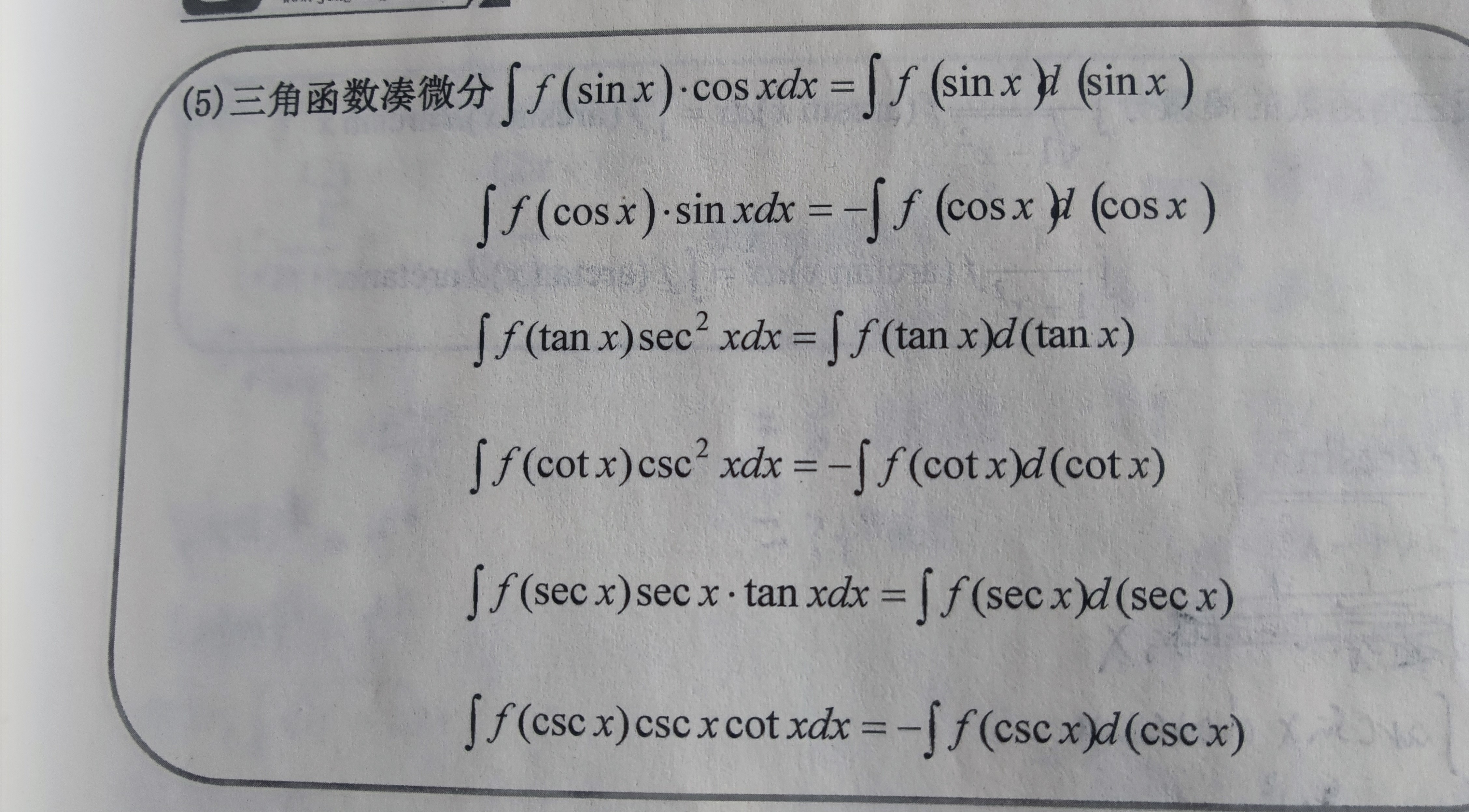

(常数凑微分:∫f(ax+b)dx=1/a∫f(ax+b)d(ax+b), 对数函数凑微分:∫f(lnx)*1/xdx=∫f(lnx)d(lnx), 指数函数凑微分, 幂函数凑微分, 三角函数凑微分, 反三角函数凑微分)






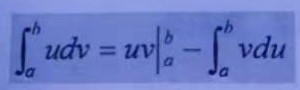









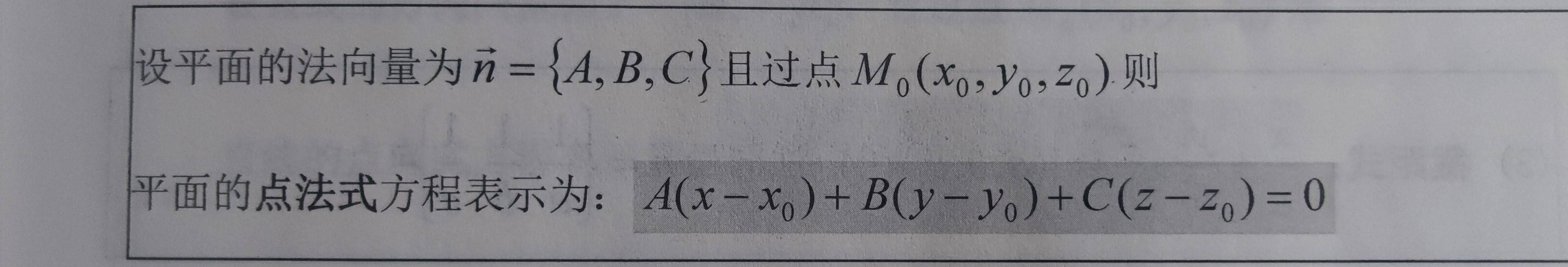

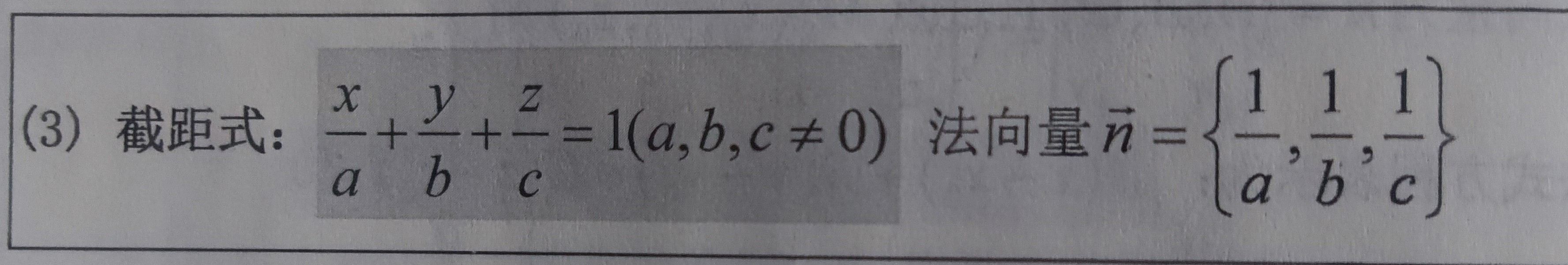


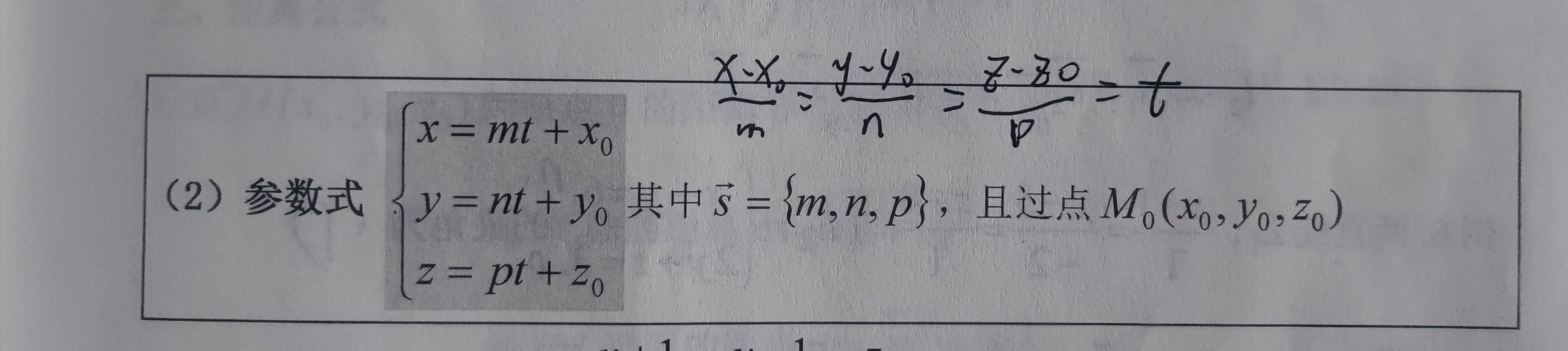
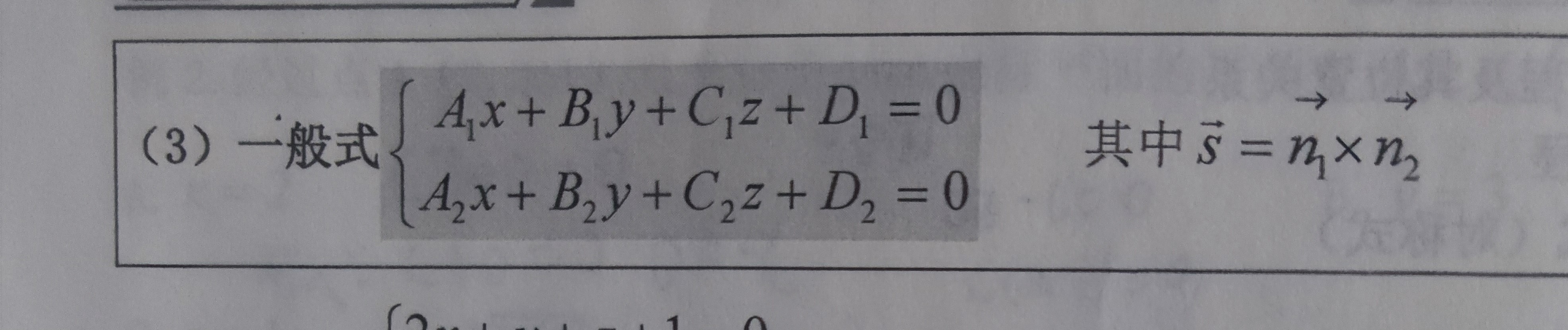



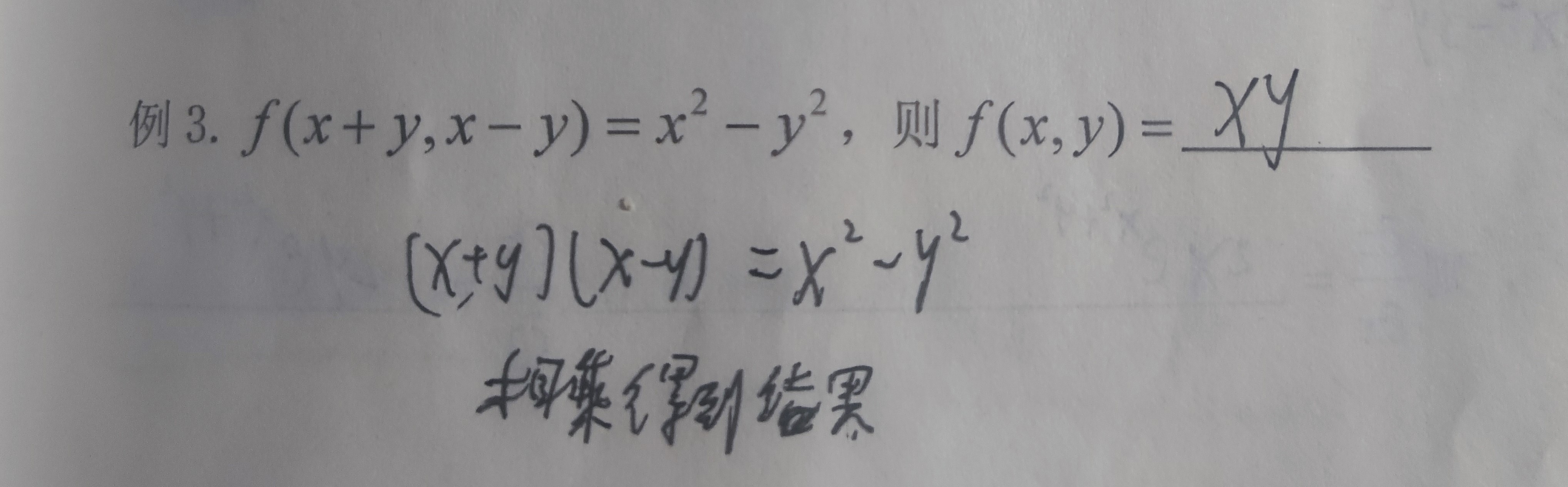
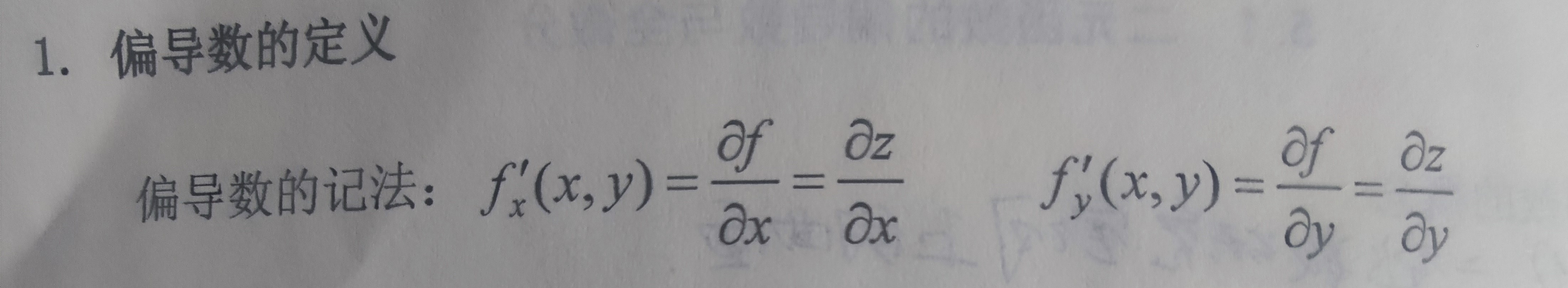

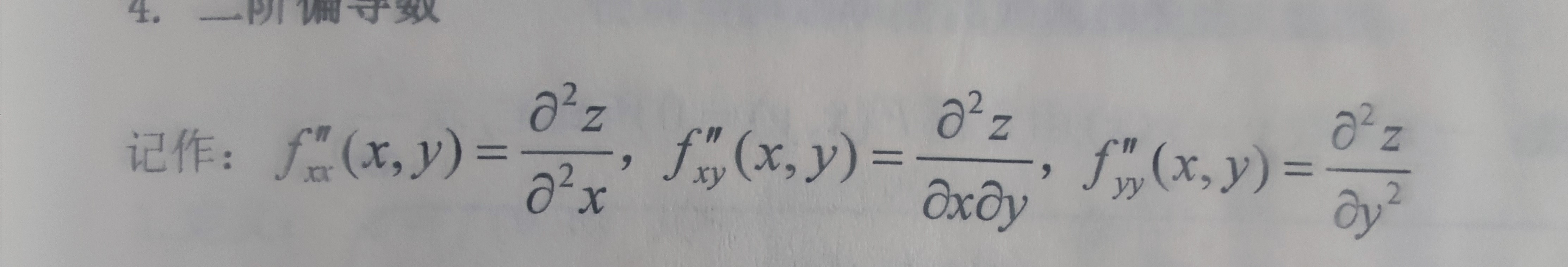







参见: 空间曲线











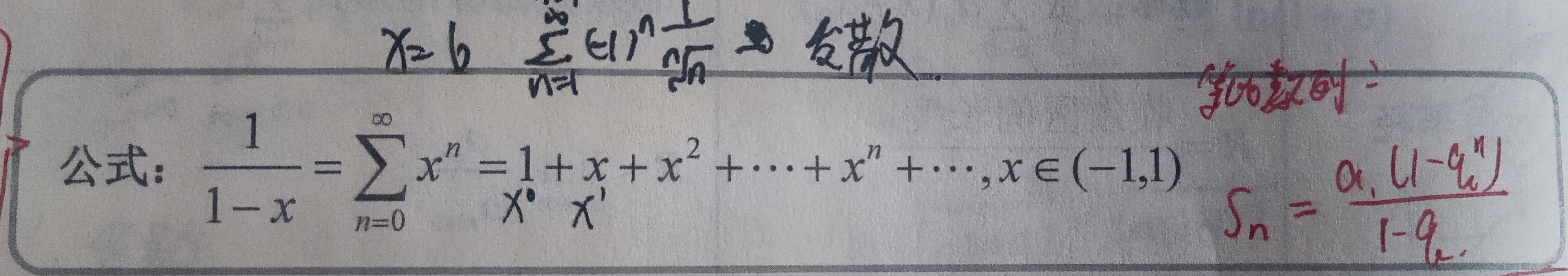

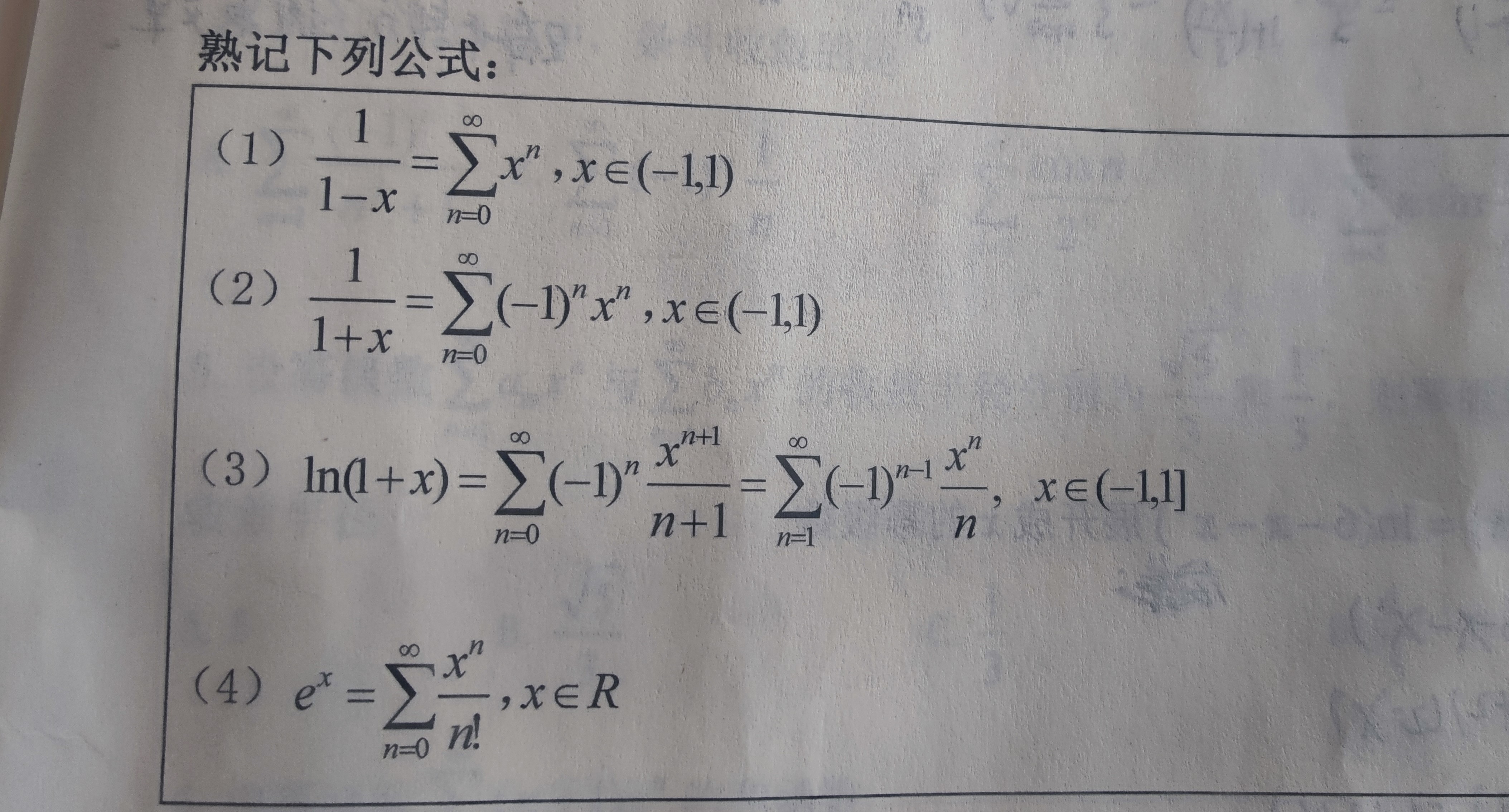


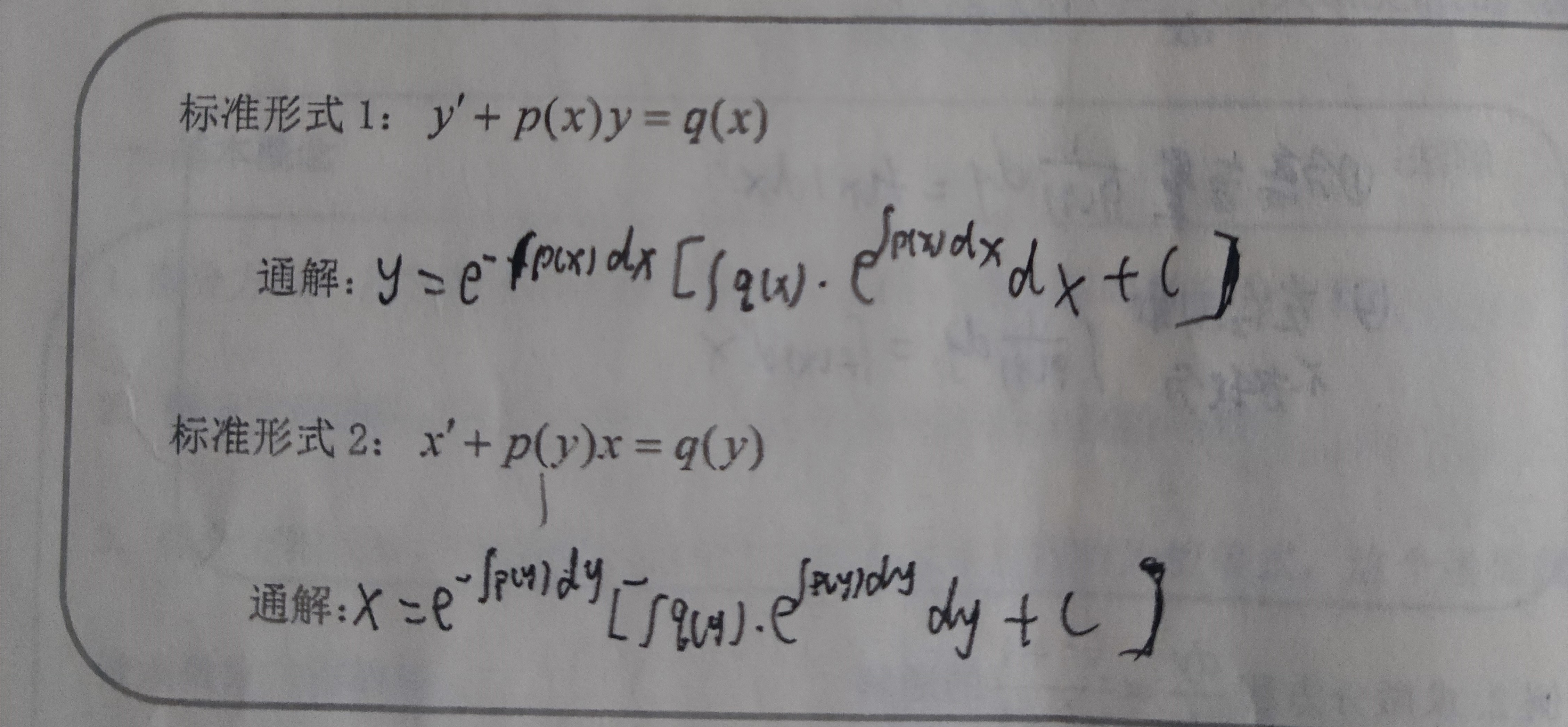





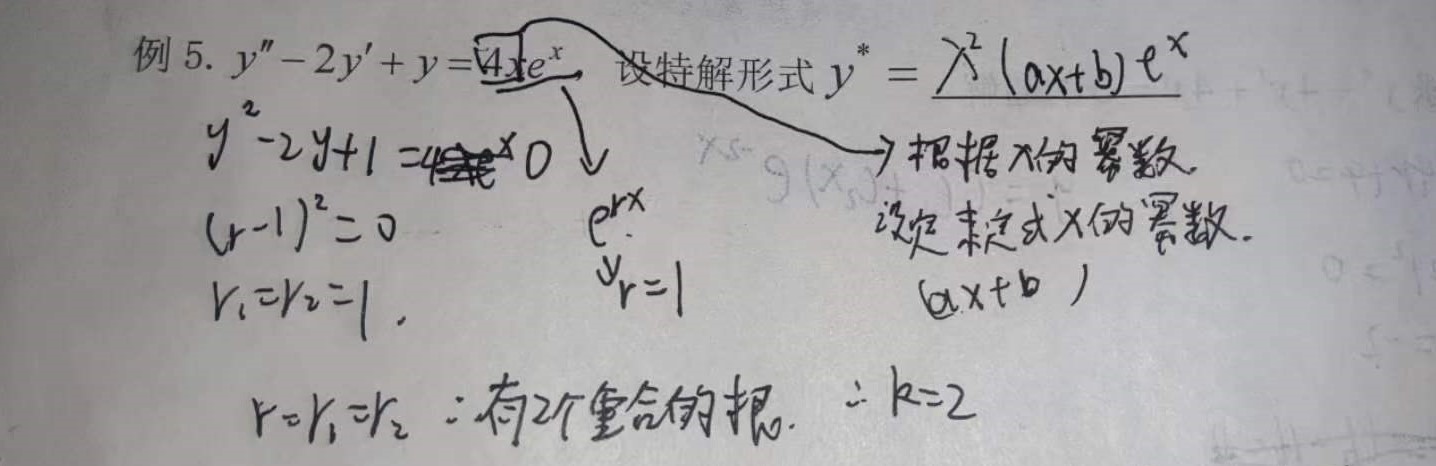
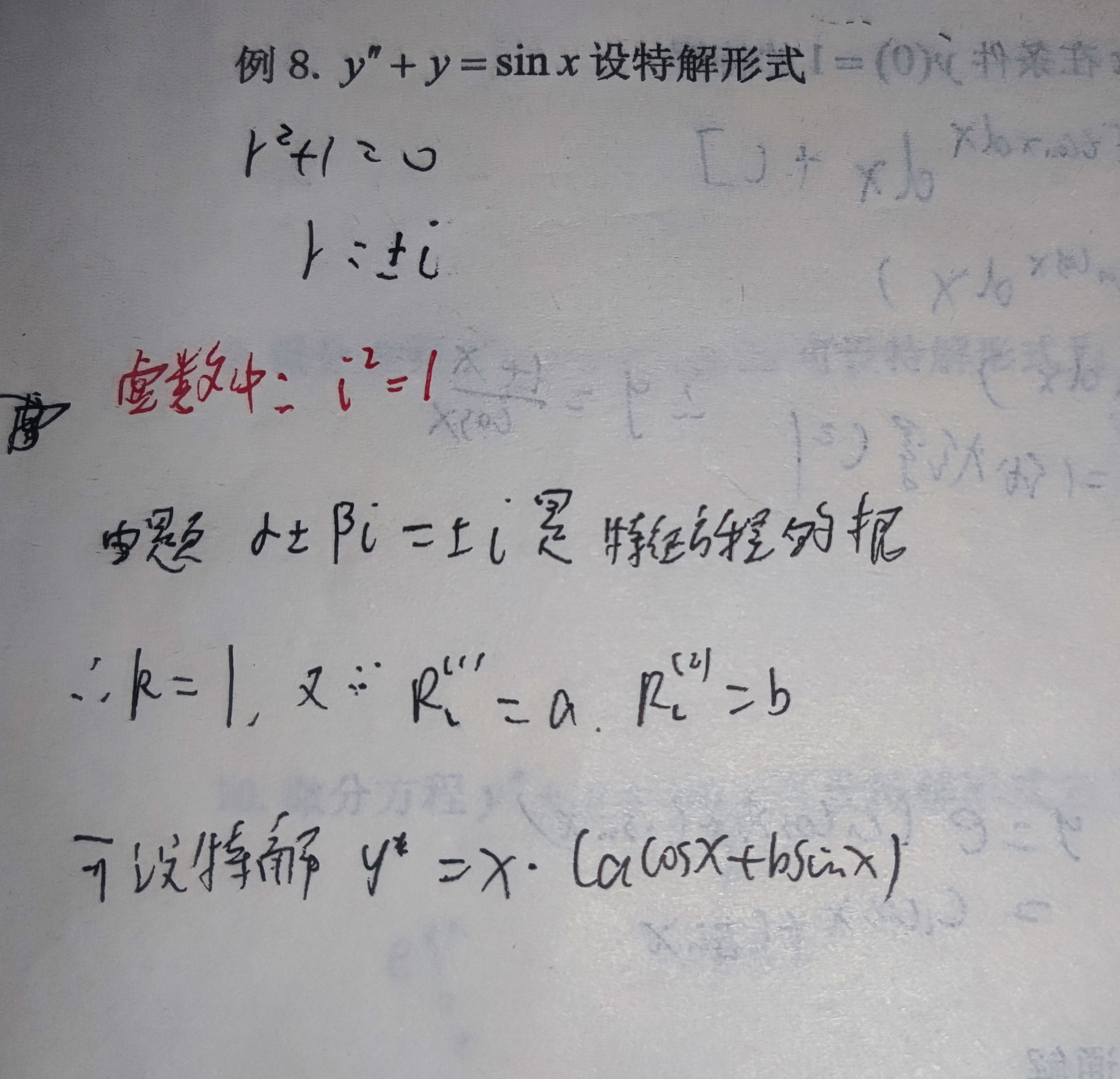
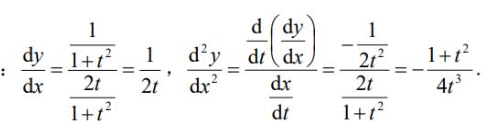

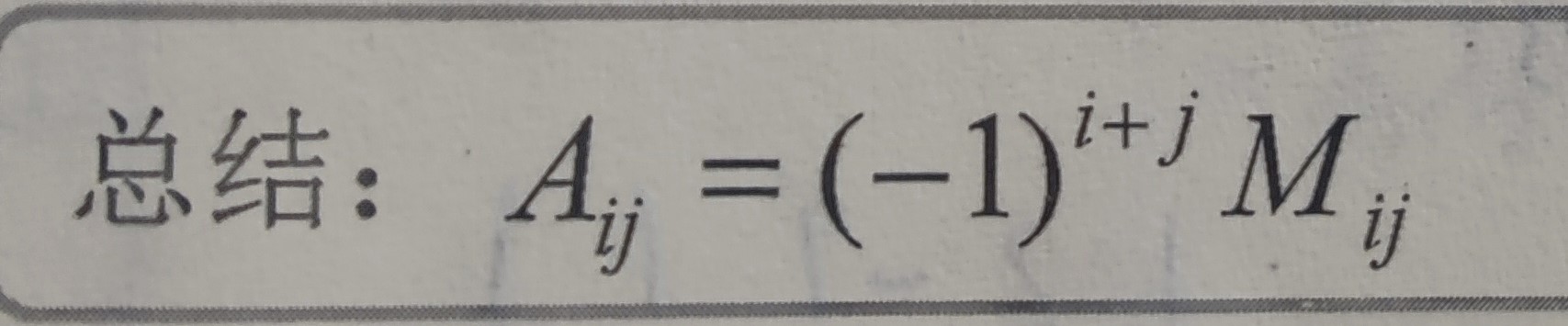
(1.D的转置与D的值相同, 2、互换行列式的两行(或两列),行列式变号 (推论:两行(或两列)完全相同的行列式值为零), 3、某一行(或列)的公因子可以提到行列式外边来 (推论:某行(或列)全为零的行列式值为零) (推论2:某行(或列)成比例的行列式值为零), 4、若行列式中某一行(或列)的元素都是两项之和,则该行列式可以按此行(或列)分拆成两个行列式之和, 5、将行列式某一行(或列)每个元素的常数倍加到另一个行(或列)相应的元素上去,其值不变)